티스토리 뷰
도입
OpenGL의 Perspective Projection 마지막 포스트입니다.
저번 2 개의 포스트를 통해 Matrix의 형태가 아래와 같다는 것까지 왔습니다.

이제 마지막으로 알아야 할 것은 Matrix의 3번째 행입니다.
보시다시피 $z_c$를 만드는 핵심 행입니다.
Z 값이 선형 변환 하지 않는 이유
앞 포스팅에서 z 값을 선형 변환하지 않는다고 설명했었습니다.
그 이유는 메모리와 정밀도 때문이라고 했습니다.
지겹겠지만 다시 한 번 이야기하면 컴퓨터 그래픽스는 3D 공간을 2D 모니터로 표현하는 일입니다.
2D 모니터는 픽셀들로 이루어져있고 각 픽셀마다 색이 값으로 정해져서 그리면 됩니다.
불투명한 물체를 볼 경우 상대적으로 카메라와 가까운 물체가 뒤에 있는 물체를 가리므로 이러한 연산을 그래픽스에서도 지원해야 합니다.
그래픽스에서는 보통 depth test라는 연산을 통해 이 연산을 지원합니다.
depth test란 픽셀 별로 depth 값을 저장하고 depth 값 비교(test)를 통해 어떤 픽셀 색이 그려질까를 결정하는 연산입니다.
문제는 애매하게 겹치는 두 개의 물체가 있을 경우 depth 값이 매우 비슷해서 어떤 픽셀은 첫번째 물체가 앞으로 나오고 어떤 픽셀은 두번째 물체가 앞으로 나오는 경우가 있다는 점입니다. 이런 경우를 z가 서로 경쟁한다 하여 z-fighting이라고 합니다.

출처: https://grandstayner.tistory.com/entry/Basic-Z-Fighting
사실 이 문제의 근본적인 문제는 컴퓨터가 실수를 완벽한 정밀도로 표현할 수 없어서 입니다.
하나의 depth 값에 조금 더 많은 비트를 할당하면 조금 더 정밀하게 값을 표현할 수 있기는 하지만 메모리가 많이 필요하다는 단점이 있습니다. 적은 메모리를 사용하고 높은 정밀도를 유지하는 것이 가장 좋은 방식인데 쉽지 않습니다.
따라서 그래픽스에서는 이런 문제를 조금이라도 해결하기 위해 z 값을 비선형으로 변환하는 방식을 이용합니다.
생각해보면 카메라와 가까운 곳은 z-fighting이 일어나면 확 티가 나지만 카메라와 멀어서 작게 보이는 곳은 z-fighting이 일어나도 잘 보이지 않을 것입니다.
그래서 z 값을 변환할 때 카메라와 가까운 곳은 값 차이가 적게 나더라도 변환 결과는 값 차이가 크게나게 하고 카메라와 먼 곳은 값 차이가 많이 나더라도 변환 결과는 값 차이가 적게 나게 합니다.
아래 그래프를 보면 조금 이해가 될 것입니다.
가로축은 변환하기 전의 z 값이고 세로축은 변환한 후의 z 값입니다.
가로축 z 값이 작은 상황에서는 기울기가 가파르지만 가로축 z 값이 큰 상황에서는 기울기가 비교적 완만합니다.
이렇게 작은 값 차이에도 큰 값 차이가 나도록 만들면 z 값이 비슷하더라도 구분이 조금 더 쉬워져서 z-fighting 현상이 줄어듭니다.
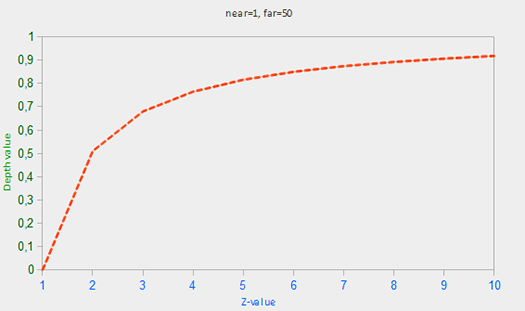
출처: https://learnopengl.com/Advanced-OpenGL/Depth-testing
조금 긴 과정을 통해 z 값을 비선형으로 변환하는 이유를 알아봤습니다.
이제 본격적으로 z 값을 변환하는 과정을 알아보겠습니다.
Perspective Projection Matrix의 3행
먼저 변환 함수의 형태와 변환 전 후의 값 범위에 대해 생각해봅시다.
변환 전의 값은 $z_e$이고 범위는 $-n$~$-f$입니다.
변환 후의 값은 $z_n$이고 범위는 $-1$~$1$입니다.
함수의 형태는 위에서 설명한 특성(비선형적)을 표현하는 형태여야 합니다.
위에서 설명한 특성을 표현하려면 함수의 형태를 $A+\frac{B}{z_e}=z_n$로 둘 수 있습니다.
이 함수는 $z_e$ 값이 작을 경우 기울기가 가파르고, $z_e$ 값이 클 경우 기울기가 완만합니다.
위 함수의 형태로 만드려고보니 공교롭게도 $w_c$(=$-z_e$)로 나눠주는 연산을 그대로 사용하면 될 것 같습니다.
($w_c$로 나누는 이유는 앞 포스팅에 설명되어있습니다.)
위 설명이 조금 헷갈릴 수 있지만 일단 진행해봅시다.
Perspective Projection Matrix의 3번째 행을 아래와 같다고 해봅시다.

z 값만 보면 $z_c=Az_e+B$가 되고 양변을 $-z_e$로 나눠주면 $z_n=-A-\frac{B}{z_e}$가 됩니다.
$A, B$ 값은 어차피 아직 결정되지 않은 수이므로 위에서 본 $A+\frac{B}{z_e}=z_n$와 같다고 볼 수 있습니다.
이제 남은 것은 $A, B$를 구하는 것입니다.
$z_e$와 $z_n$의 관계를 알고 있으므로 $z_n=-A-\frac{B}{z_e}$식에 각각 대입해서 A, B를 구합시다.
먼저 $z_e$가 $-n$일 때 $z_n$이 $-1$이라는 정보를 이용하면 아래와 같은 식이 나옵니다.
$-1=-A-\frac{B}{-n}$
그 다음으로 $z_e$가 $-f$일 때 $z_n$이 $1$이라는 정보를 이용하면 아래와 같은 식이 나옵니다.
$1=-A-\frac{B}{-f}$
두 식을 빼면 $B=\frac{2fn}{n-f}$가 됩니다.
구한 $B=\frac{2fn}{n-f}$을 위 식에 대입합니다.
마지막 A를 구하면 $A=\frac{-(f+n)}{f-n}$가 됩니다.
$A$와 $B$를 행렬에 대입하면 결국 matrix의 최종 형태는 아래와 같습니다.

지금까지 오랜 과정을 통해 Perspective Projection Matrix를 구해냈습니다.
사실 OpenGL에서도 glm 라이브러리를 사용하거나 Unity를 이용하면 Matrix의 형태를 알지 못해도 Perspective Projection을 할 수 있고 파라미터 값을 조절해서 원하는 효과를 낼 수 있습니다.
하지만 알고 사용하는 것과 모르고 사용하는 것은 분명히 차이가 있다고 생각합니다.
처음 배울 때는 시간이 오래 걸리긴 하지만 한 번 이해하고 나면 잘 까먹지 않을 것입니다.
레퍼런스
z 값이 linear하지 않은 이유를 설명하는 자료입니다.
https://learnopengl.com/Advanced-OpenGL/Depth-testing
learnopengl.com
'수학&물리' 카테고리의 다른 글
| 순열, 조합, 중복 순열, 중복 조합 (2/5) (0) | 2025.08.22 |
|---|---|
| 순열, 조합, 중복 순열, 중복 조합 (1/5) (0) | 2025.08.16 |
| OpenGL의 Perspective Projection (2/3) (2) | 2020.04.01 |
| OpenGL의 Perspective Projection (1/3) (0) | 2020.03.12 |
| 열역학 자료 6: 점성, 열전도율, 확산에 대하여 3 (0) | 2020.01.31 |
- Total
- Today
- Yesterday
- opengl
- 루빅스큐브
- Unreal
- 유니티
- 통계학
- 경우의 수
- RubiksCube
- Mesh Processing
- RL
- collision detection
- Scriptable Render Pipeline
- value type
- VTK
- 최적화
- CollisionDetection
- 순열
- 조합
- MeshProcessing
- normalized device coordinate
- 수학
- 중복 조합
- AABB
- 값 형식
- Unity
- C#
- Mesh
- 참조 형식
- perspective projection
- DirectX12
- 중복 순열
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
