티스토리 뷰
도입
오늘은 저번 포스트에 이어 OpenGL에서 Perspective Projection을 다루는 Matrix에 대해 알아보겠습니다.
이번에는 본격적으로 Matrix의 각 원소에 대해서 알아보고 저번 시간에 다루지 못했던 자세한 내용에 대해서도 알아보겠습니다. 바로 이 포스트를 읽으면 이해가 어려우니 저번 포스트를 먼저 읽으시길 바랍니다.
View Frustum
가장 먼저 Matrix를 만들려면 View Frustum이 어떤 Parameter들을 통해 정의되는지 알아야 합니다.
Frustum은 두 가지 데이터셋 중 하나의 형태로 정의할 수 있습니다.
*여기서 데이터셋을 통해 정의될 수 있다는 말은 데이터셋의 값을 알면 유일한 형태를 만들 수 있다는 뜻입니다. 예를 들어 3개의 정점의 위치를 알면 삼각형의 형태를 알아낼 수 있죠.
일단 나열해보자면
첫 번째 데이터셋은 left, right, bottom, top, near, far를 해서 총 6개이고
두 번째 데이터셋은 aspect ratio(종횡비)와 field of view(시야각), near, far해서 총 4개입니다.
둘 중 어떤 데이터셋을 이용하더라도 유일하게 view frustum의 형태를 정의할 수 있습니다.
두 데이터 셋의 개수가 다른 이유는 두 번째 데이터셋으로 정의하는 것이 첫 번째 데이터셋으로 정의하는 것보다 암시적으로 의미하고 있는 것이 더 많기 때문입니다.
이 외에도 두 데이터 셋 모두 암시적으로 의미하는 것이 더 있습니다.
그것은 바로 두 데이터 셋 모두 원점에서 해당 평면으로 퍼져나간다는 정보가 있다는 것이지요.
첫 번째 데이터 셋
이론으로만 설명하면 어려우니 예제를 통해서 설명해보겠습니다.
예를 들어 left=-3, right=5, bottom=-3, top=3, near=-2, far=-6이라고 해봅시다.
여기서 left, right는 x 축 값이고, bottom, top는 y 축 값이고, near, far는 z 축 값입니다.

그림을 보면 알 수 있듯이 left, right, bottom, top, near 값을 통해 정사각형의 평면을 정의할 수 있습니다.
이 평면을 near plane이라고 합니다.
near 값이 0이 아니라면 원점에서 이 정사각형의 각 꼭짓점으로 향하는 4개의 선을 그릴 수 있습니다.
4개의 선을 z값이 far까지 되도록 이은 후 만들어진 평면을 far plane이라고 합니다.
마지막으로 4개의 선, near plane, far plane을 이용해 조합한 도형이 바로 View Frustum입니다.
두 번째 데이터 셋
첫 번째 데이터 셋의 경우 near plane의 중앙이 z 축에 있어야한다는 제약이 있지 않았습니다.
즉 left, right, top, bottom 값에 따라 near plane이 z 축 기준으로 오른쪽이나 위쪽으로 치우칠 수 있다는 말이지요.
하지만 두 번째 데이터 셋으로 표현하면 기본적으로 near plane의 중앙이 z 축에 있다고 가정합니다.
따라서 aspect ratio(종횡비)와 field of view(시야각), near 값을 통해 near plane을 정의할 수 있습니다.
첫 번째 데이터 셋을 기준으로 설명할 것이기 때문에 두 번째 데이터 셋에 대해서는 깊이 다루지 않겠습니다.
Perspective Projection Matrix의 형태
이제 본격적으로 Matrix의 형태를 알아봅시다.
좀 내용이 길고 중간 중간 매끄럽지 않은 부분이 있지만 쭉 한 번 읽어보고 다시 읽어보시면 이해가 될 겁니다.
먼저 NDC의 x, y의 값을 결정할 1행과 2행을 생각해봅시다.
조금 생각해보면 near plane에 찍힐 정점들의 x, y 값을 구하면 쉽게 NDC의 x, y 값을 결정할 수 있다는 것을 알 수 있습니다. 왜냐하면 near plane이 결국 x 값이 -1~1, y 값이 -1~1인 NDC의 앞 쪽 평면으로 바뀔 것이기 때문입니다.
문제를 좀 더 단순하게 생각해서 먼저 y 값을 구해봅시다.
+x 위치에서 -x 방향으로 View Space를 바라보면 아래 이미지와 같습니다.
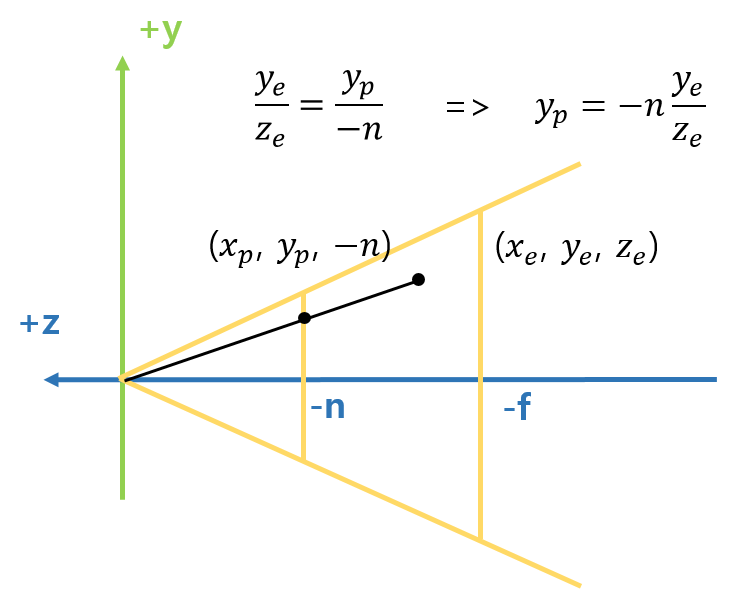
near plane의 z 값은 -n, far plane의 z 값은 -f 입니다. (n, f는 양수입니다)
아래처럼 삼각비를 이용하면 손 쉽게 near plane에 찍힐 y 값을 구할 수 있습니다.
$(x_e, y_e, z_e)$는 eye space에서의 정점이고 $(x_p, y_p, -n)$은 projection된 점입니다.
$x_e, y_e, z_e$와 $n$은 알고 있는 값이고 구해야 하는 값은 $x_p, y_p$입니다.
식 자체는 쉽게 나왔지만 조금 문제가 있습니다.
위 식을 이용하면 단순한 코딩을 통해 $y_p$ 값을 구할 수 있습니다.
하지만 이 식을 행렬과 벡터의 곱만으로 표현할 수 없습니다.
$y_p$은 $y_e$값과 $z_e$의 영향을 받습니다. $y_e$를 곱하는 것은 행렬 곱으로 표현할 수 있지만 $z_e$를 나누는 연산은 하나의 행렬 곱으로 표현할 수 없습니다.
따라서 OpenGL은 $z_e$로 나누는 과정을 두 단계로 나눠서 진행합니다.
각 단계는
1) 행렬 곱을 통해 $z_e$ 값을 다른 곳에 저장하는 것과
2) 저장한 $z_e$ 값으로 나누는 것 입니다.
행렬 곱을 통해 $z_e$ 값을 저장할 때는 $(x_e, y_e, z_e)$를 $(x_e, y_e, z_e, 1)$로 만들어 사용합니다.
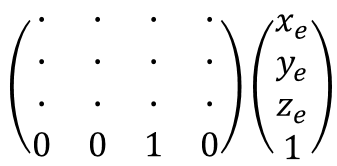
행렬을 위처럼 만들면 연산 결과 벡터의 마지막 항으로 $z_e$값이 저장되는 것이지요
또한 저번 포스트에서 말했듯이 Camera Space에서 NDC로 넘어갈 때 z축이 뒤집어지는 점을 유의해야 합니다.
그래서 이 과정까지 한 번에 하기 위해 행렬을 아래와 같이 만듭니다.

중간 점검 - 문자 및 연산 과정 정리
이로써 Matrix의 4번째 행을 구했습니다.
앞으로 이어질 내용이 조금 어렵게 느껴질 수 있으므로 지금까지의 결과와 앞으로 나올 변수에 대해서 한 번 정리하겠습니다.
먼저 벡터는 $(x_e, y_e, z_e, w_e)$, $(x_c, y_c, z_c, w_c)$, $(x_n, y_n, z_n)$가 있고 벡터끼리의 관계는 아래와 같습니다.
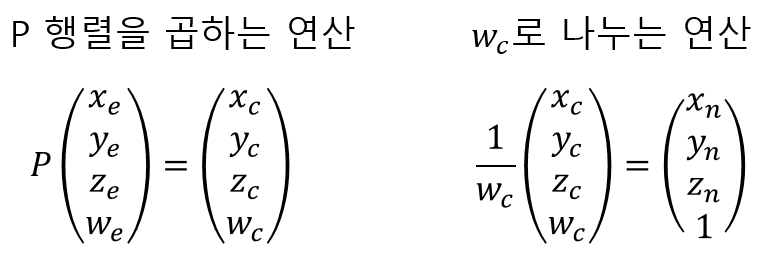
여기서 P 행렬은 구하고 있는 Perspective Projection Matrix입니다.
가장 먼저 eye space의 점 $(x_e, y_e, z_e, w_e)$ 입니다. 이 값은 알고 있습니다. 값의 범위 자체는 제한이 없습니다. $w_e$의 값은 1입니다. 통일성을 위해 문자로 표현했습니다.
다음은 clip space의 점 $(x_c, y_c, z_c)$ 입니다. 저번 포스트에서는 clip space와 NDC를 같은 것이라고 설명했었습니다. 위 두 연산을 하나로 합쳐서 생각하면 그렇지만 P의 형태를 제대로 알기 위해서는 두 연산을 나눠야 하기 때문에 나눠서 표현했습니다. clip space 점의 값의 범위는 $-w_c$~$w_c$입니다. 이 범위를 넘어가는 점들은 잘립니다. P 행렬의 4번째 행을 통해 $w_c$=$-z_e$라는 것을 알았습니다. 역시 통일성을 위해 $w_c$로 표현했습니다.
마지막은 ndc의 점 $(x_n, y_n, z_n)$ 입니다. 값의 범위는 각 원소마다 -1~1입니다.
위 그림에서 P행렬을 곱하는 연산은 Vertex Shader에서 코딩으로 하고, $w_c$로 나누는 연산은 OpenGL에게 맡깁니다. 따라서 저희의 목표는 $w_c$에 제대로 된 값이 들어가고 $w_c$로 나누었을 때 제대로 ndc의 점이 나오도록 P의 형태를 만드는 것입니다.
앞에서 $x_p$, $y_p$를 언급했었는데 이 점은 P 행렬의 1, 2행을 구하기 위해 잠깐 쓰인 문자라고 생각하시면 됩니다.
Perspective Projection Matrix의 1, 2행
이제 다시 본격적으로 행렬의 2번째 행을 알아보겠습니다.
먼저 $y_p$와 $y_n$의 관계를 살펴봅시다.
$(x_p, y_p, -n)$은 near plane에 projection된 점이고 $(x_n, y_n, z_n)$은 NDC의 점이므로
$y_p$와 $y_n$의 관계는 [$b$~$t$]에서 [$-1$~$1$]로 가는 변환입니다.
Scale과 Translate로 이루어진 변환이죠.
$y_p$와 $y_n$을 각각 축으로 그래프에 그려 두 값 사이의 변환을 알아내봅시다.

이제 $y_n=Ay_p+B$ 함수의 A, B 값을 구하는 문제로 왔습니다.
$y_p$ 값이 b일 때 $y_n$ 값이 -1, $y_p$ 값이 t일 때 $y_n$ 값이 1이라는 정보를 이용해서 A를 구합니다.
각각 대입하고 두 식을 연립방정식으로 풀면 $A=\frac{2}{t-b}$임을 알 수 있습니다.
알게 된 A 값과 한 점을 이용해 B 값을 구하면 $B=-\frac{t+b}{t-b}$입니다.
구한 A 값과 B 값을 이용하여 $y_n=Ay_p+B$에 대입하면 아래와 같은 식이 나옵니다.
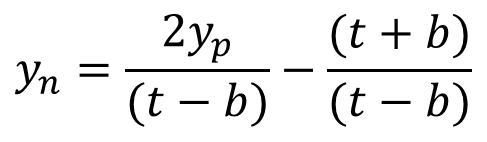
앞에 나온 $y_p=-n\frac{y_e}{z_e}$식을 대입하면 아래와 같은 식이 나옵니다.

마지막으로 $-z_e$로 나누는 과정이 나중에 있을 것이기 때문에 식을 $\frac{식}{-z_e}$의 형태로 바꿔야 합니다.

$-z_e$로 나누는 것은 Vertex Shader에서 Fragment Shader로 넘어갈 때 자동으로 해주기 때문에 행렬에 넣을 필요가 없습니다. 따라서 분자만 생각해서 행렬을 다시 만들면 행렬의 2번째 행은 아래와 같습니다.
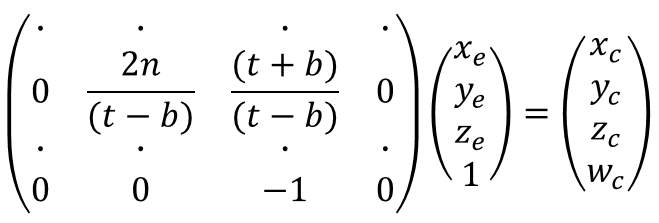
x도 비슷한 방법이기 때문에 따로 설명하지 않겠습니다.
그럼 지금까지 과정을 통해 행렬의 1,2,4번째 row가 결정되었습니다.

나머지 해야할 일은 3번째 row를 결정하는 일입니다.
3번째 row도 별로 어려울 일 없이 [$-n$~$-f$]에서 [$-1$~$1$]로 가도록 값을 채우면 될거 같습니다.
하지만 OpenGL에서는 그렇게 하지 않습니다.
간단히 z 값은 fragment의 앞 뒤를 결정하므로 매우 높은 정밀도를 요구하는데 x, y처럼 [$-n$~$-f$]에서 [$-1$~$1$]로 선형 변환하면 메모리상 비효율적이기 때문입니다.
메모리 이득을 보려면 눈에 잘 보이는 곳에 높은 정밀도를 주고 눈에 잘 안 보이는 먼 곳에 상대적으로 적은 정밀도를 주면 됩니다.
자세한 내용은 이어지는 포스팅에서 설명하겠습니다.
요약
지금까지의 과정을 통해 Matrix의 형태를 거의 알아냈습니다.
한 번 읽고 이해하기 어려운 내용이므로 이해가 안되더라도 천천히 반복해서 읽어보시길 바랍니다.
이번 포스팅의 내용을 요약하면 아래와 같습니다.
1. View Frustum은 두 종류의 데이터 셋으로 정의할 수 있다.
2. View Space에서 NDC의 변환은 Matrix 곱과 $-z_e$를 나누는 2개의 과정으로 이루어진다.
3. $-z_e$로 나누는 과정은 OpenGL에서 이루어지므로 이것을 염두에 두고 Matrix를 만들면 된다.
4. Matrix의 1, 2행은 삼각비를 이용해 구할 수 있다.
5. View Space에서 NDC로 갈 때 z의 변환은 선형 변환이 아니다.
다음 포스팅에서는 Perspective Projection Matrix의 최종 형태를 설명드리겠습니다.
'수학&물리' 카테고리의 다른 글
| 순열, 조합, 중복 순열, 중복 조합 (1/5) (0) | 2025.08.16 |
|---|---|
| OpenGL의 Perspective Projection (3/3) (0) | 2020.04.15 |
| OpenGL의 Perspective Projection (1/3) (0) | 2020.03.12 |
| 열역학 자료 6: 점성, 열전도율, 확산에 대하여 3 (0) | 2020.01.31 |
| 열역학 자료 5: 점성, 열전도율, 확산에 대하여 2 (0) | 2020.01.31 |
- Total
- Today
- Yesterday
- 참조 형식
- 통계학
- 루빅스큐브
- opengl
- DirectX12
- C#
- AABB
- perspective projection
- MeshProcessing
- Unreal
- value type
- 중복 순열
- 값 형식
- 중복 조합
- 수학
- RubiksCube
- 순열
- normalized device coordinate
- VTK
- collision detection
- Mesh Processing
- 조합
- CollisionDetection
- 유니티
- 최적화
- Mesh
- Unity
- 경우의 수
- RL
- Scriptable Render Pipeline
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
