티스토리 뷰
앞 포스팅에서 캐릭터의 표면을 이루는 정점들이 뼈대에 속해있고 뼈대의 움직임에 따라 정점들을 움직임으로써 애니메이션을 구현한다는 것을 이야기했습니다.
또 뼈대를 계층 구조로 만들면 팔만 움직이거나 손만 움직이거나 하는 애니메이션을 구현할 수 있다고 이야기했죠.
이론상으로는 간단해 보이지만 우리는 컴퓨터에게 규칙을 알려줘야 하기 때문에 수식을 통해 위와 같은 상황을 표현해야겠죠.
그래픽스를 해본 여러분이라면 변환(Transformation)에 대해서 알고 계실 겁니다.
Transformation은 두 개의 관점으로 볼 수 있습니다.
첫 번째 관점은 한 공간 안에 있는 모든 정점들을 특정 규칙에 따라 움직이는 연산으로 생각하는 것이고
두 번째 관점은 하나의 가만히 있는 정점에 대해 다른 좌표계에서 바라보도록 만드는 연산으로 생각하는 것입니다.
아래와 같은 Transformation에 대해 생각해보겠습니다.

첫 번째 관점대로 해석하면 위 Transformation은
아래의 이미지처럼 (x, y)에 있던 정점을 (x+3, y+2)=(x', y') 위치로 이동시키는 Transformation입니다.
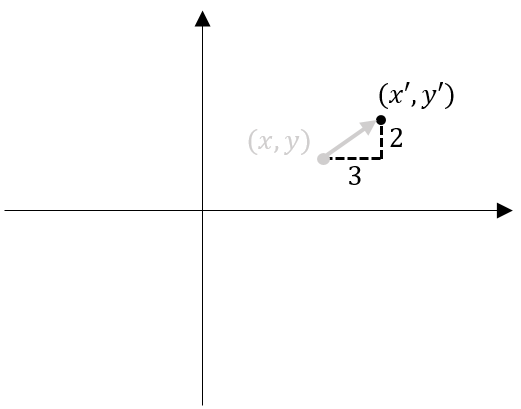
반면 두 번째 관점대로 해석하면 위 Transformation은
아래의 이미지처럼 원래의 좌표계를 기준으로 (-3, -2) 지점에 원점을 두고 좌표축의 방향이 같은 좌표계에서
원래의 정점을 바라보게 만드는 Transformation입니다.

두 번째 관점을 좀 더 자세히 설명드리기 위해 예를 들어 설명해보겠습니다.
*설명의 편의를 위해 Translation과 Rotation만을 이용했습니다.
목표
A 좌표계에서 (x, y)로 정의된 갈색 정점을 B 좌표계에서는 어떻게 정의되는지 알고 싶다고 해봅시다.
(단, A 좌표계와 B 좌표계 사이의 변환은 단순히 Translation과 Rotation 만으로 가능합니다.)
알고 있는 것
A 좌표계에서 정의된 갈색 정점 위치 (x, y)
A 좌표계에서 정의된 B 좌표계의 원점 위치(Ox, Oy)와 축의 방향(Ux, Uy), (Vx, Vy), 축의 방향 벡터 U와 V는 단위 벡터

이미지가 많이 복잡합니다.
가장 먼저 오른쪽 (x, y) 위치에 있는 갈색 점에 대해서 생각해봅시다.
A 좌표계 기준으로 보면 이 점은 1사 분면에 위치해 있지요.
그 다음은 고개를 왼쪽으로 살짝 갸우뚱하여 B 좌표계와 맞춘 후 B 좌표계를 기준으로 이 점을 봅시다.
이번에는 이 점이 B 좌표계의 2사 분면에 위치해 있지요. (가로 방향으로는 살짝 왼쪽이고 세로 방향으로는 좀 더 위쪽)
우리의 목표는 이 점에 특정한 Transformation을 취해서 A 좌표계의 2사 분면에 위치한 점이 되도록 하는 것입니다.
이 특정한 Transformation은 Transformation을 바라보는 관점에서 설명했듯이, 점을 옮기는 Transformation으로 볼 수도 있고 A 좌표계에서 바라보던 점을 B 좌표계에서 바라보도록 하는 것일 수도 있습니다.
Transformation에 대한 첫 번째 관점이 좀 더 직관적이므로 첫 번째 관점으로 해석하여 정점을 A 좌표계의 2사 분면으로 옮겨봅시다.
먼저 두 좌표계의 원점을 일치시키는 Translation을 정점에 취해야 합니다.
Translation 후의 결과는 다음과 같습니다.

그 후 두 좌표계의 기저 벡터를 맞추기 위해 U 벡터를 (1, 0) 벡터로 옮기는 회전을 해야 합니다.
회전을 하고 나면 이동이 끝난 회색 정점은 검은 색 정점의 위치로 가게 됩니다.

A 좌표계에서 정의된 검은 정점은, B 좌표계에서 정의된 갈색 정점과 같은 위치 값을 가진다고 보시면 됩니다.
지금까지 이 특정한 Transformation을 첫 번째 관점으로 해석했습니다.
같은 Transformation을 두 번째 관점으로 해석하면 A 좌표계에서 정의되었던 갈색 정점을 B 좌표계에서 정의되도록 하는 것이지요.
장황하게 설명했지만 사실 A 좌표계에서 정의되었던 정점을 B 좌표계에서 정의하려면
단순히 A 좌표계 축을 B 좌표계 축으로 맞추는 회전 행렬 R,
A 좌표계 원점을 B 좌표계 원점으로 이동시키는 이동 행렬을 T라고 했을 때, TR의 역행렬 즉, $(TR)^{-1}$을 곱하면 됩니다.
아무튼 지금까지 Transformation을 바라보는 관점에 대해 설명했습니다.
그래픽스 분야에서 자주 쓰이는 MVP(Model, View, Projection) Transformation 중 MV(Model, View) Transformation은 두 번째 관점으로 해석하는 것이 좋습니다.
Model 좌표계에서 정의되었던 정점들을 Model Matrix를 곱함으로써 World 좌표계로,
World 좌표계에서 정의되었던 정점들을 View Matrix를 곱함으로써 Camera 좌표계로 옮기게 되는거죠.
이 포스팅에서 Transformation의 두 번째 관점에 대해 이토록 자세히 설명한 이유는 스켈레톤 애니메이션에서도 똑같은 방식을 사용하기 때문입니다.
단순히 지금까지 다뤘던 Model, World, Camera 좌표계 외에 Bone 좌표계라는 새로운 좌표계가 생긴 것 뿐이죠.
Bone 좌표계는 각 Bone 마다 가지고 있습니다.
Bone 좌표계에서 정점을 정의하면 보다 손쉽게 Bone에 붙어있는 정점들의 움직임을 만들 수 있기 때문입니다.
그 외에도 앞 포스팅에서 말했듯이 하나의 정점은 여러 개의 Bone의 영향을 받을 수도 있다고 하였습니다.
복수 개의 Transformation Matrix의 영향을 받아 Transformation하는 정점은 간단하게 다음과 같이 쓸 수 있습니다.
예를 들어 정점 V가 Transformation A에 0.8 영향을 받고 Transformation B에 0.2 영향을 받아 V'으로 움직인다면 아래처럼 간단한 수식으로 표현할 수 있는거죠.
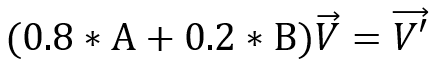
지금까지 Bone 좌표계와 여러 Bone Transformation의 영향을 받는 정점에 대해 이야기했습니다.
어떻게 그것이 구현되는지는 다음 글에서 설명하겠습니다.
'프로그래밍 > OpenGL' 카테고리의 다른 글
| OpenGL 및 Assimp를 활용한 스켈레톤 애니메이션 프로그래밍 (3/3) (0) | 2019.08.31 |
|---|---|
| OpenGL 및 Assimp를 활용한 스켈레톤 애니메이션 프로그래밍 (1/3) (0) | 2019.08.29 |
- Total
- Today
- Yesterday
- Unreal
- CollisionDetection
- collision detection
- AABB
- C#
- Unity
- normalized device coordinate
- MeshProcessing
- value type
- 참조 형식
- RubiksCube
- 중복 순열
- 중복 조합
- 값 형식
- 경우의 수
- 순열
- Mesh
- Scriptable Render Pipeline
- 통계학
- 루빅스큐브
- perspective projection
- VTK
- 최적화
- DirectX12
- Mesh Processing
- RL
- 수학
- 조합
- opengl
- 유니티
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
